A Noob’s Guide to Linear Regression: Build your own linear regression model with few lines and impress your Professors!
Learn Linear Regression Just Like a Friend Would Teach You: Simple, Friendly, and Effective
Why Linear regression
From stock predictions to deducing relationships between bank loans and credit scores, there is always some sort of relationship between entities. The calories you eat to how big you are, the price of a product to the number of customers for that product, or how broke you are to how many friends you have 😭—there is a presence of linear relationships between various entities. Linear regression understands the relationship between these entities and creates a model so that you can predict how much money you need in your bank account to make friends(highly unlikely though) . But in hindsight it helps you determine the value of an unknown entity using the value of the known entity, given they are related.
Prerequisites:
Simple math
Python basics
Lil’ bit of common sense
1. In the Beginning…..
Here’s a more polished version of the introduction:
Let’s use a simple dataset showing the maximum and minimum temperatures for a particular day.
In the dataset below, df represents the data with the following columns:
tmax: Maximum temperaturetmin: Minimum temperaturetmax_tomorrow: Temperature for tomorrow
This dataset can help us predict tomorrow’s temperature based on the maximum and minimum temperatures of today.
Now, let’s explore the relationship between tmax (today’s maximum temperature) and tmax_tomorrow (tomorrow’s maximum temperature) to see if we can predict tomorrow’s temperature based on today’s. Essentially, we want to determine if knowing today’s maximum temperature helps us forecast tomorrow’s. This way, you can decide whether it’s worth grabbing that polar bear ice cream for tomorrow! 🍦
2. Understanding the data
If you notice above, I’ve plotted tmax against tmax_tomorrow. You can see there’s a linear relationship between them: as tmax increases, tmax_tomorrow also increases. This is a perfect demonstration of linear regression in action!
3. Math…..
If you hadn’t daydreamed during your 6th-grade math class and had actually paid attention, you would have learned an interesting formula y=mx+c
The formula y=mx+c\ helps find a point y using three values: x (the point on the x-axis), c (the y-intercept), and m (the slope of the line). This is known as the line equation, as it determines the value of y for any given x on the line. Linear regression builds on this concept. Given our data, we can draw a straight line through the scatterplot of our data to model the relationship between tmax and tmax_tomorrow.
Wow, a straight line through the data! This means that, theoretically, using the line equation, we can predict tmax_tomorrow based on tmax. But is linear regression done? Not quite. The line drawn above is just to illustrate a linear relationship. It doesn’t accurately model the data yet. If we use this line to predict tmax_tomorrow, we may get significant differences from the actual values. This discrepancy between the actual and predicted values is known as the loss. Our goal is to minimize this loss so that our model closely matches the actual values.
y=mx+c
Returning to the formula y=mx+c we know x and y, but m (the slope) and c (the y-intercept) are not predefined—they are variables we need to determine. The process involves trying out different values for m and c until we find the combination that minimizes the loss. The goal of linear regression is to adjust m and c so that the predicted values are as close as possible to the actual values, thereby minimising the loss.
4. Finale
There are two ways of determining m and c values of the above equation. Gradient descent(which is super complicated for an introductory blog and will definitely be covered in later blogs) and least squared error which is essentially like “linear regression for middle schoolers” version. Lets stick to the latter.
Least square error find the values of m and c that produces the least square. hence the name least square error (definitely a lot of time went into naming that!)
The above are the formulas to find m(slope) and c(intercept) so we use all data points to find values of m and c that reduces the loss function. If you want to understand the above formulas in detail you can refer to this article by a very reputable and profitable educational institution that goes in detail with least squared error here.
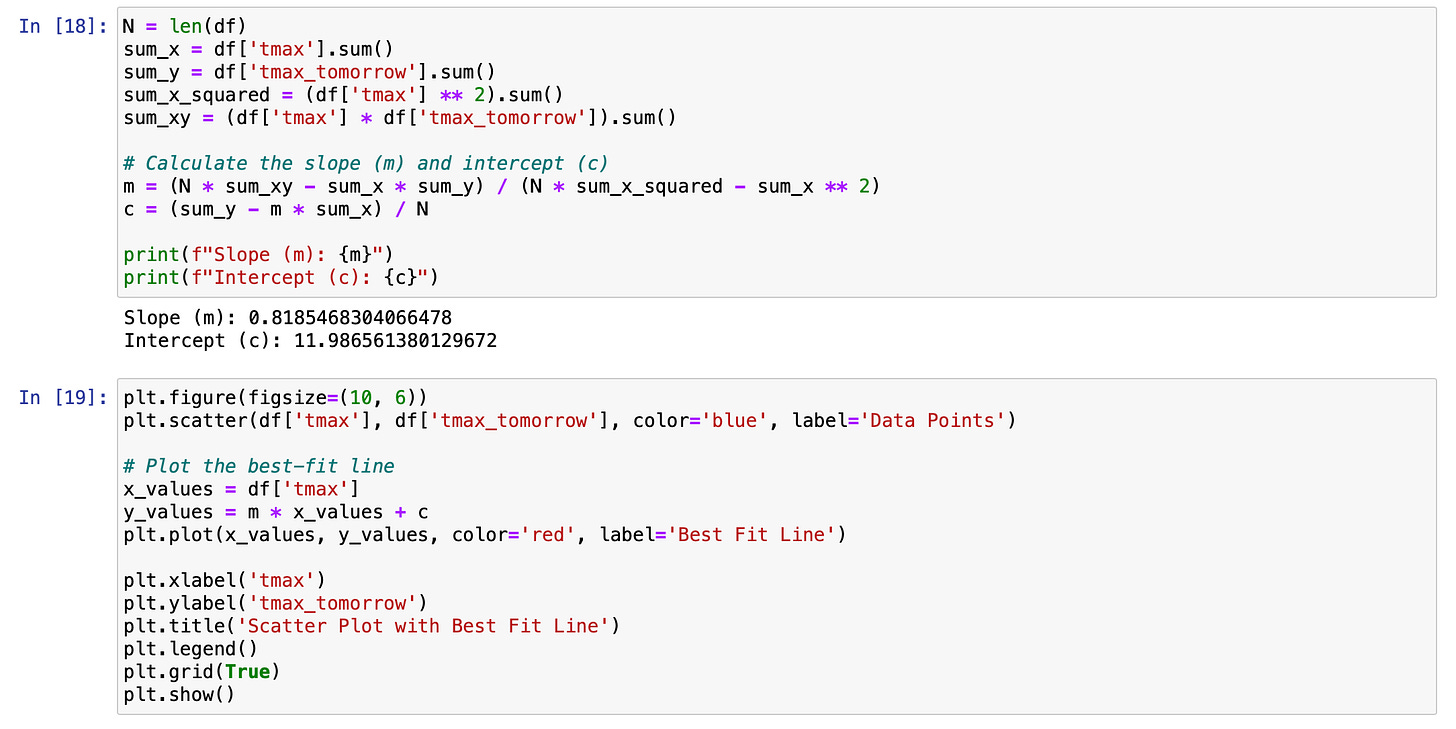
Putting the above formula into code and seeing the values.
The red line you see is essentially our line of best fit. By using the least-squares method, we determined the optimal values for mmm (slope) and ccc (y-intercept) that minimize the loss. This line represents the best approximation of the relationship between our variables, reducing the discrepancies between the predicted and actual values as much as possible.
4. Conclusion
You’re now significantly smarter! 🎓 Subscribe to the newsletter for more detailed breakdowns on neural networks, blockchain, AR/VR, and more. I’ll explain these topics in simple terms so you can understand them easily. Until then, keep breathing eating 🍔!
(But trust us on the “subscribe” buttons!)









👏🏻👏🏻👏🏻